数据结构与算法-排序

# 数据结构与算法 - 排序

排序算法演示网站：https://visualgo.net/zh/sorting

# 排序介绍

一旦我们将数据放置在某个数据结构中存储起来后(比如数组)，就可能根据需求对数据进行不同方式的排序

比如对姓名按字母排序
对学生按年龄排序
对商品按照价格排序
对城市按照面积或者人口数量排序
对恒星按照大小排序

由于排序非常重要而且可能非常耗时，所以它已经成为一个计算机科学中广泛研究的课题，人们已经研究出一套成熟的方案来实现排序。学习已有的排序方法是非常有必要的。

# 冒泡排序

# 冒泡排序思路

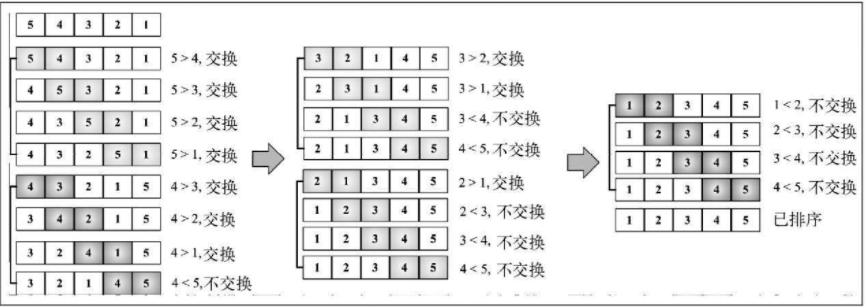
对未排序的元素从头到尾依次进行两两比较
首先选取第1个元素和第2个比较，如果第一个元素大，则交换位置；否则不交换
然后后移动一位，选择第2个和第3个进行比较，依次类推，当一轮比较完成，最大的在未排序元素的最右边，成为已排序元素。
重复上面步骤，每一轮都会少一个待排序元素，直至所有元素排序完成

# 冒泡排序实现

/**
 * 冒泡排序
 */
function bubbleSort(arr) {
  // 外层循环：根据元素个数，决定几轮冒泡
  for (let i = arr.length - 1; i > 0; i--) {
    for (let j = 0; j < i; j++) {
      // 内层循环：每轮比较相邻元素的大小
      if (arr[j] > arr[j + 1]) {
        swap(arr, j, j + 1)
      }
    }
  }

  return arr
}

代码分析

通过两层循环来实现冒泡排序：

外层循环：控制一共需要多少轮冒泡；每轮排序都排除掉已经排序的元素。
- 第一轮排序，冒泡到最后一个length - 1
- 第二轮排序，冒泡到倒数第二个元素lenght - 2
内层循环：根据每轮冒泡未排序元素个数，确定每轮冒泡，相邻元素的比较次数
- 第一次比较，0和1；
- 第二次比较，1和2；以此类推

排序1

交换元素位置swap函数代码如下：

/**
 * 交换元素位置
 * @param {*} arr 
 * @param {*} idxA 
 * @param {*} idxB 
 */
function swap(arr, idxA, idxB) {
  [arr[idxA], arr[idxB]] = [arr[idxB], arr[idxA]]
}

# 冒泡排序效率

比较次数： $$O(n^2)$ $

第一次比较n - 1次，第二次比较n-2次，......最后一次比较1次
那么比较次数就是 $$(n - 1) + (n - 2) + ... + 1 = \frac{n(n - 1)}{2}$ $，即$ $O(n^2)$ $

交换次数： $$O(n^2)$ $

每次比较有需要交换和不需要两种可能，如果每两次比较需要一次交换，那么交换次数就是 $$\frac{n(n - 1)}{2} / 2 = \frac{n(n - 1)}{4}$ $ 即 $$O(n^2)$ $

# 选择排序

选择排序改进了冒泡排序，将交换的次数由O(N²)减少到O(N)，但是比较的次数依然是O(N²)

# 选择排序思路

选择第1个索引位置元素，然后依次与后面元素比较
比较过程中，如果第i个位置元素比第1个小，记录i位置索引
每次比较都记录最小索引，一轮比较结束后，交换首次选出的待比较元素与最小元素的位置
后移一位选择待比较元素，重复步骤，直到所有元素比较完毕

# 选择排序实现

/**
 * 选择排序
 */
function selectionSort(arr) {
  // 外层循环：每次初始化标记最小元素位置索引
  for (let i = 0; i < arr.length - 1; i++) {
    let min = i
    for (let j = i + 1; j < arr.length; j++) {
      // 内层循环：记录一轮循环中，未排序的元素中最小元素位置索引
      if (arr[min] > arr[j]) {
        min = j
      }
    }
    // 最小元素位置索引不等于每次循环初始值 i 本身
    // 说明最小元素在后面，交换原i位置元素和min位置元素 
    if (i !== min) swap(arr, i, min)
  }

  return arr
}

代码分析

通过两层循环来实现冒泡排序：

外层循环：每次初始化标记最小元素位置索引
内层循环：记录一轮循环中，未排序的元素中最小元素位置索引
最小元素位置索引不等于每次循环初始值 i 本身，说明最小元素在后面，交换原i位置元素和min位置元素

# 选择排序效率

比较次数： $$O(n^2)$ $

比较次数同冒泡排序，都为 $$\frac{n(n - 1)}{2}$ $，即$ $O(n^2)$ $

交换次数： $$O(n)$ $

交换次数未 $$n - 1$ $，即$ $O(n)$ $
所以通常认为选择排序在执行效率上是高于冒泡排序的

# 插入排序

插入排序思想的核心是局部有序。

比如在一个队列中的人，我们选择其中一个作为标记的队员。这个被标记的队员左边的所有队员已经是局部有序的。
这意味着，有一部分人是按顺序排列好的。有一部分还没有顺序。

# 插入排序思路

首先取出一个元素，认为该元素左边的元素已经是有序的。第一次取第一个元素
从已选择元素的右侧取出一个新元素，然后从后向前依次与已排序元素进行比对
如果本次选取已排序元素大于新元素，则向前移动一位继续选取已排序元素与新元素比对
直到找到已选取元素小于新元素，将新元素插入到这个后面
重复以上步骤直到所有元素排序完毕

# 插入排序实现

/**
 * 插入排序
 */
function insertionSort(arr) {
  // 外层循环：每次选出待排序元素
  for (let i = 1; i < arr.length; i++) {
    const element = arr[i] // 选出待排序元素

    let j = i // 记录新插入位置 默认在原位置
    while (j > 0 && arr[j - 1] > element) {
      // 后移前一个元素
      arr[j] = arr[j - 1]
      j-- // 更新插入位置
    }
    // 插入元素到索引j位置
    arr[j] = element
  }
}

代码分析

通过两层循环实现插入排序：

外层循环：取出待插入（排序）元素
- 从1开始，默认0位置已排序好
- 选出待排序元素，暂存到element
内层while循环：确定插入位置
- 如果前面元素大于待插入元素，将前面的元素后移一位
- 更新插入位置j--

# 插入排序效率

比较次数： $$O(n^2)$ $

第一次最多比较1次，第二次最多比较2次，...... 最后一次最多比较n - 1次
那么最多比较次数就是 $$(n - 1) + (n - 2) + ... + 1 = \frac{n(n - 1)}{2}$ $
但并不是每次插入都需要这么多次比较，可能只比较一次就插找到了插入位置
所以平均只有全体比较次数的一半， $$\frac{n(n - 1)}{2} / 2 = \frac{n(n - 1)}{4}$ $
复杂度虽然仍是 $$O(n^2)$ $，但平均情况下，相对于选择排序，比较次数少了一半。
也就是说，插入排序最差情况下比较次数等于选择排序和冒泡排序

复制次数： $$O(n^2)$ $

第一次最多复制1次，第二次最多复制2次，...... 最后一次最多复制n - 1次
那么最多复制次数就是 $$(n - 1) + (n - 2) + ... + 1 = \frac{n(n - 1)}{2}$ $
平均复制次数是 $$\frac{n(n - 1)}{2} / 2 = \frac{n(n - 1)}{4}$ $

交换次数： $$O(n)$ $

交换次数为外层循环次数

对于基本有序的情况

对于已经有序或基本有序的数据来说，插入排序要好很多。
当数据有序的时候，while循环的条件总是为假，所以它变成了外层循环中的一个简单语句，执行N-1次
在这种情况下，算法运行至需要N(N)的时间，效率相对来说会更高
另外别忘了，我们的比较次数是选择排序的一半，所以这个算法的效率是高于选择排序的

# 希尔排序

希尔排序，也称递减增量排序，是插入排序的一种更高效的改进版本。

希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布。
希尔算法首次突破了计算机界一直认为的**算法的时间复杂度都是 $$O( n^2)$ $**的大关，为了纪念该算法里程碑式的意义，用Shell来命名该算法

回顾插入排序：

在插入排序执行到一半的时候，标识符左边这部分数据项都是排好序的，而标识符右边的数据项是没有排序的
此时，取出指向的那个数据项，把它存储在一个临时变量中；接着，从刚刚移除的位置左边第一个单元开始，每次把有序的数据项向右移动一个单元，直到存储在临时变量中的数据项可以成功插入

插入排序的问题：

假设一个很小的数据项在很靠近右端的位置上，这里本来应该是较大的数据项的位置
把这个小数据项移动到左边的正确位置，所有的中间数据项都必须向右移动一位
如果每个步骤对数据项都进行n次复制，平均下来是移动n/2，N个元素就是n²/2，所以我们通常认为插入排序的效率是 $$O(n^2)$ $
如果有某种方式，不需要一个个移动所有中间的数据项，就能把较小的数据项移动到左边，那么这个算法的执行效率就会有很大的改进，希尔排序实现了这种方法

# 希尔排序思路

希尔排序主要通过对数据进行分组实现快速排序

首先确定一个增量gap，按序列增量进行分组
根据设定的增量gap将序列分为gap个组，每组再进行局部的插入排序
排序完成后，减小增量gap，每组再进行局部单独排序，直至gap减小到1，进行最后一次排序即可。

整个排序过程和插入排序思路相同，区别在于，比较后希尔排序元素可能需要移动gap，插入排序每次移动1。gap为1时，就是插入排序。

排序2

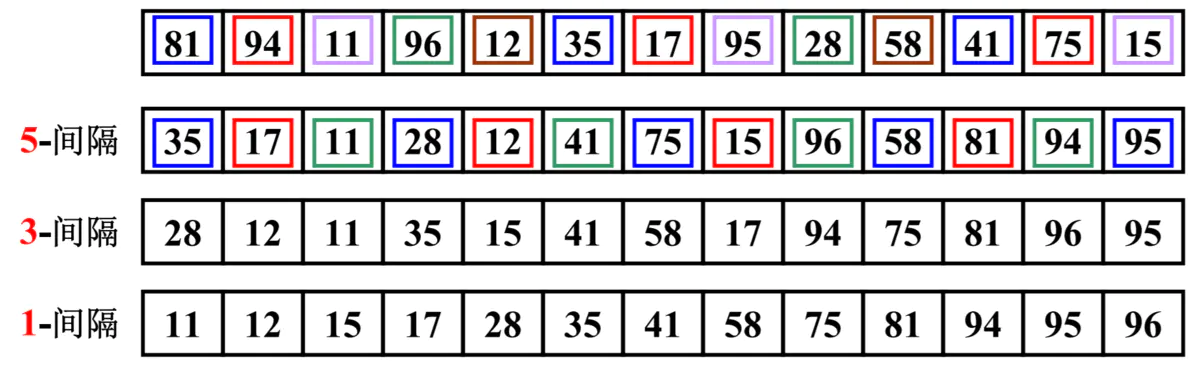
如上图：81, 94, 11, 96, 12, 35, 17, 95, 28, 58, 41, 75, 15.

我们先让间隔为5分组，同颜色为一组，得到 (81, 35, 41)、(94, 17, 75)、(11, 95, 15)、(96, 28)、(12, 58)
分组插入排序后的新序列，一定可以让数字离自己的正确位置更近一步
再让间隔位3，得到(35, 28, 75, 58, 95)、(17, 12, 15, 81)、(11, 41, 96, 94)
分组插入排序后的新序列，让数字离自己的正确位置又近了一步
最后，我们让间隔为1，也就是所有数据看成一组进行插入排序，这时，数字都离自己的位置更近，那么需要复制的次数一定会减少很多

增量gap选择

原始序列：

希尔排序原稿中，他建议的初始间距是N / 2，简单的把每趟排序分成两半
也就是说，对于N = 100的数组，增量间隔序列为: 50、25、12、6、3、1
最坏时间复杂度是 $$O(n^2)$ $

Knuth增量序列：

{1, 4, 13, 40 ...}，多项式为 $$\frac{1}{2}(3^k-1)$ $
最坏时间复杂度是 $$O(n^\frac{3}{2})$ $

Hibbard增量序列：

{1, 3, 5, 7 ...} ，多项式为 $$2^k - 1$ $
这种增量的最坏复杂度为 $$O(n^\frac{3}{2})$ $；猜想的平均复杂度为$ $O(n^\frac{5}{4})$ $，未被证明

Sedgewick增量序列：

{1, 5, 19, 41, 109 ...}，该序列的多项或是 $$9 * 4^i - 9 * 2^1 + 1$ $或是$ $4^i - 3 * 2^i + 1$ $
猜想：最坏复杂度为 $$O(n^\frac{4}{3})$ $，平均复杂度为$ $O(n^\frac{7}{6})$ $

# 希尔排序实现

/**
 * 希尔排序
 */
function shellSort(arr) {
  // 普通增量序列
  // let gap = Math.floor(arr.length / 2) // 默认增量

  // Knuth增量序列
  let gap = 1
  while (gap < arr.length / 3) { // gap 1, 4, 13, 40 ...
    gap = gap * 3 + 1
  }

  // 第一层循环：while循环，使gap不断减小
  while (gap > 0) {
    // 第二层循环：插入排序 以gap为增量，进行分组，对分组进行插入排序
    // 每组从第二个开始排序，默认第一个为有序的
    for (let i = gap; i < arr.length; i++) {
      let element = arr[i]

      // 第三层循环：确定插入位置
      let j = i
      while (j >= gap && arr[j - gap] > element) {
        arr[j] = arr[j - gap] // 每次元素后移gap
        j -= gap
      }

      arr[j] = element
    }

    // 普通增量 重新计算增量
    // gap = Math.floor(gap / 2)
    // Knuth增量 重新计算增量
    gap = (gap - 1) / 3
  }

  return arr
}

代码分析：

首先确定gap增量，第一层循环控制增量不断减小，直至gap = 1
第二层循环，以gap为增量，进行分组，对分组进行插入排序
第三层循环：确定插入位置，元素需要后移时，后移gap长度

# 希尔排序效率

希尔排序的效率和增量有直接关系

原稿中的增量效率都高于简单排序，最坏时间复杂度 $$O(n^2)$ $
Knuth增量序列，最坏时间复杂度是 $$O(n^\frac{3}{2})$ $
Hibbard增量序列，最坏时间复杂度为 $$O(n^\frac{3}{2})$ $
Sedgewick增量序列，最坏复杂度为 $$O(n^\frac{4}{3})$ $

# 快速排序

快速排序可以说是目前所有排序算法中，最快的一种排序算法。当然，没有任何一种算法是在任意情况下都是最优的。但是，大多数情况下快速排序是比较好的选择。

快速排序的核心思想是分而治之，先选出一个数据（比如65），将比其小的数据都放在它的左边，将比它大的数据都放在它的右边。这个数据称为枢纽。

# 快速排序思路

在待排序的数据集中，选择一个数作为枢纽pivot
所有小于基准pivot的元素放在枢纽pivot的左边；所有大于基准的元素放在右边
对基准左右两边的子集不断重复上面两个步骤，直到所有子集只剩下一个元素为止

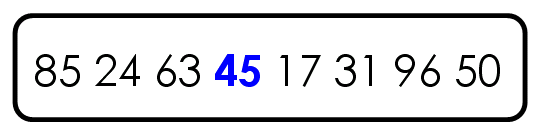
比如，现在有一个数据集{85, 24, 63, 45, 17, 31, 96, 50}，怎么对其排序呢？

第一步，选择中间的元素45作为枢纽（其实可以任意选择有的直接选择第一个元素，之后讨论如何选择枢纽）
第二步，按照顺序，将每个元素与枢纽进行比较，形成两个子集，一个"小于45"，另一个"大于等于45"。

排序4

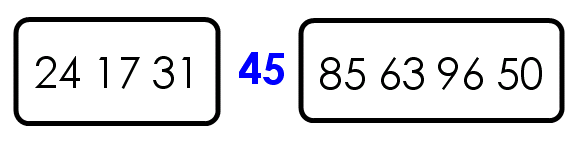
第三步，对两个子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

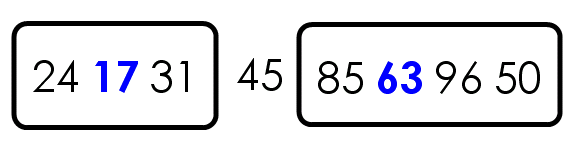
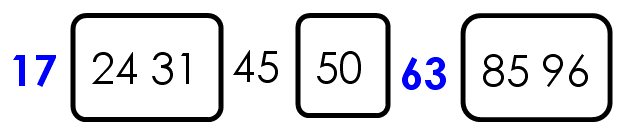
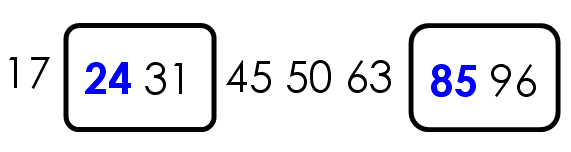
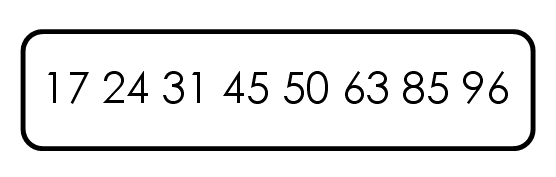
枢纽选择

一种方案是直接选择第一个元素作为枢纽，但第一个作为枢纽在某些情况下，效率并不是特别高
第二种是使用随机数，随机取枢纽，但是随机函数本身就是一个耗性能的操作
第三种比较优秀的解决方案是：取头、中、尾的中位数。例如 8、12、3的中位数就是8

# 快速排序实现

/**
 * 快速排序 - 获取枢纽
 *  - 选择中位数作为枢纽
 * @param {*} left 最左侧索引
 * @param {*} right 左右侧索引
 */
function getPivot(arr, left, right) {
  const center = Math.floor((left + right) / 2)

  // 排序选中的左、中、右三个数，由大到小
  if (arr[left] > arr[center]) {
    swap(arr, left, center)
  }
  if (arr[center] > arr[right]) {
    swap(arr, center, right)
  }
  if (arr[left] > arr[center]) {
    swap(arr, left, center)
  }

  // 中位数与倒数第二个数交换位置 倒数第一的数一定比中位数大，直接当作放在右边
  swap(arr, center, right - 1)

  // 返回选择的枢纽pivot
  return arr[right - 1]
}

/**
 * 快速排序
 * @param {*} arr 待排序数组
 * @param {*} left 待排序数组最左边索引
 * @param {*} right 待排序数组最右边索引
 * @returns
 */
function quickSort (arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    // 获取枢纽
    const pivot = getPivot(arr, left, right)

    // 创建两个指针
    let l = left // 左边指向最左
    let r = right - 1 // 右边指向倒数第二个 枢纽的位置
    while (l < r) {
      while (arr[++l] < pivot) {} // 右移左指针到大于pivot的位置
      while (arr[--r] > pivot) {} // 左移右指针到小于pivot的位置
      if (l < r)  swap(arr, l, r) // 左指针索引小于右指针 交换左右指针指向的元素位置
    }

    // 交换左指针指向的元素和枢纽元素
    swap(arr, l, right - 1)

    // 左、右子集递归
    quickSort(arr, left, l - 1)
    quickSort(arr, l + 1, right)
  }

  return arr
}

有集合，{23, 4, 76, 10, 72, 7, 99, 12, 13}，过程如下图所示：

排序10

(a) 首先9个元素，从0开始
(b) 找出中位数(left + right) / 2，即(0 + 8) / 2 = 4
(c) 对找出的三个元素进行排序，然后交换中位数23与倒数第二个元素12的位置
(d) 初始化左右两个指针，分别指向要排序的第一个元素13和最后一个要排序的元素23即中位数
(e) 右移左指针找到第一个比中位数23大的元素76，左移右指针找到第一个比中位数23小的元素7，交换这两个元素
(f) 继续右移左指针找到比中位数23大的元素76，再左移右指针，找到比中位数23小的元素12，此时left = 5; right = 4; left >= right;，停止查找
(g) 交换left = 5的元素76与中位数23的位置，即完成此次中位数的左右分割
(h) 23左侧和右侧分别为小于和大于它的元素子集。
(i) 子集重复上面步骤，完成排序

# 快速排序效率

快速排序的最坏情况效率

每次选择的枢纽都是最左边或者最右边的，那么效率等同于冒泡排序
上面的实现方法不可能遇到最坏的情况，因为是三个值中选择中位值

快速排序的平均效率

快速排序的平均效率是 $$O(nlogn)$ $

# 堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列
小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列

# 堆排序思路

将数据集合创建成最大堆
创建成最大堆后，最大值会被存储在数组的第一个位置，将这个值与堆的最后一个值交换位置，堆的大小减1；那么最大值就已经排好顺序
然后将堆的根节点下移堆化，再创建现有对数据的最大堆，重复步骤2，直到堆的大小为1

# 堆排序实现

对于给定位置index的节点：

它的左子节点的位置是index * 2 + 1（如果位置可用）；
它的右侧子节点的位置是 index * 2 + 2（如果位置可用）；
它的父节点位置是 (index - 1) / 2，向下取整（如果位置可用）。

/**
 * 下移堆化 大顶堆
 * @param {*} arr 
 * @param {*} index 
 * @param {*} heapSize 
 */
function heapify(arr, index, heapSize) {
  let largest = index

  const left = index * 2 + 1
  const right = index * 2 + 2

  if (left < heapSize && arr[left] > arr[index]) {
    // 左子节点更大
    largest = left
  }
  if (right < heapSize && arr[right] > arr[largest]) {
    // 再比对 右子节点更大
    largest = right
  }

  if (largest !== index) {
    swap(arr, index, largest) // 交换位置
    // largest位置此时为原index位置的节点，可能比子节点小，再进行堆化
    heapify(arr, largest, heapSize)
  }
}

/**
 * 堆排序
 */
function heapSort(arr) {
  // 构建堆 从最后一个父节点位置开始
  for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {
    heapify(arr, i, arr.length)
  }

  let heapSize = arr.length
  while (heapSize > 1) {
    swap(arr, 0, --heapSize) // 交换最大值和堆的最后一个值，然后堆大小减1
    heapify(arr, 0, heapSize) // 重新下移堆化
  }

  return arr
}

理解了二叉堆，堆排序的代码很简单，不再分析。

问题

构建堆时，i的初始值是Math.floor(arr.length / 2) - 1，这是最后一个非叶子节点的索引，为什么呢？

我们假设数组长度为n，最后一个父节点序号是i，分两种情形考虑：

情况1：堆的最后一个非叶子节点若只有左子节点
- 左子节点为n - 1，又是i * 2 + 1，那么n - 1 = i * 2 + 1即i = (n - 1) / 2 - 1
情况2：堆的最后一个非叶子节点有左右两个子节点
- 左子节点是n - 2，那么n - 2 = i * 2 + 1即i = (n - 1) / 2 - 1
- 右子节点是n - 1，那么n - 1 = i * 2 + 2即i = (n - 1) / 2 - 1
- 两个节点的父节点i都是i = (n - 1) / 2 - 1

很显然，当完全二叉树最后一个节点是其父节点的左孩子时，树的节点数为偶数；

当完全二叉树最后一个节点是其父节点的右孩子时，树的节点数为奇数。

JS中如果除不尽就向下取整，那么(n - 1) / 2 - 1就是n / 2 - 1。

# 堆排序效率

堆排序的平均时间复杂度为 $$Ο(nlogn)$ $

# 归并排序

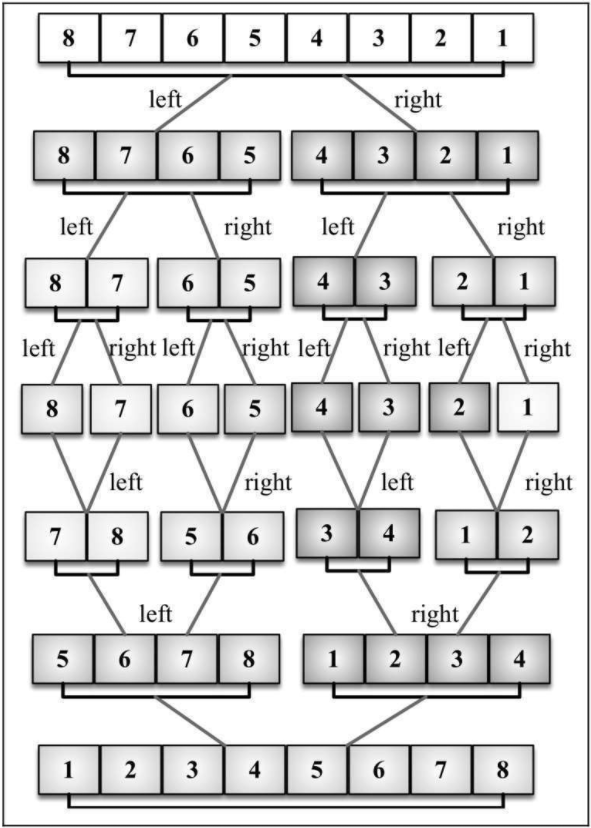
归并排序的核心思想是分而治之，将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

# 归并排序思路

将待排序集合等分成两份，然后再将子集进行分割，依此分割，直到每个子集只有一个元素
接着将分割的两个子集合并成大的子集，依此合并，直到最后合并成一个数组

排序11

# 归并排序实现

/**
 * 合并两个数组
 * @param {*} lArr
 * @param {*} rArr
 * @returns
 */
function merge(lArr, rArr) {
  const result = []
  while (lArr.length > 0 && rArr.length > 0) {
    result.push(lArr[0] < rArr[0] ? lArr.shift() : rArr.shift())
  }

  return result.concat(lArr, rArr)
}

/**
 * 归并排序
 * @param {*} arr 
 * @returns 
 */
function mergeSort(arr) {
  if (arr.length > 1) {
    const midIndex = Math.floor(arr.length / 2)

    // 递归 分割数组
    const lArr = mergeSort(arr.splice(0, midIndex))
    const rArr = mergeSort(arr)
    // 数组合并
    arr = merge(lArr, rArr)
  }

  return arr
}

# 归并排序效率

堆排序的平均时间复杂度为 $$Ο(nlogn)$ $

# 计数排序

计数排序是分布式排序。分布式排序使用已组织好的辅助数据结构——桶，然后进行合并，得到排序好的数组。

计数排序是一个整数排序算法，空间取决于最大的数字。

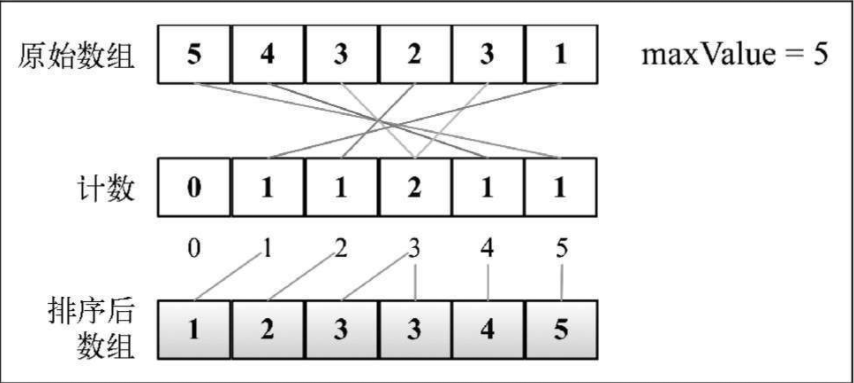
# 计数排序思路

统计排序数组中最大值，使用最大值作为桶的最大索引来创建数组
遍历排序数组，将数组中元素值作为桶的索引，对应桶索引计数加1
此时元素已在桶中排好序，遍历取出桶中元素不为0的索引，依次放入到排序数组中即可

# 计数排序实现

/**
 * 计数排序
 */
function countingSort(arr) {
  // 找到最大值 作为 最大索引
  // let max = arr[0]
  // for (let i = 1; i < arr.length; i++) {
  //   if (max < arr[i]) {
  //     max = arr[i]
  //   }
  // }
  let max = Math.max(...arr) // 最大值 作为 最大索引

  // 创建桶 根据arr的最大值，创建数组用于计数
  const buckets = new Array(max + 1).fill(0)
  for (let element of arr) {
    buckets[element]++
  }

  // 迭代buckets数组并构建排序后的结果数组
  let sortedIndex = 0 // 元素排序后的索引位置 默认0开始
  for (let i = 0; i < buckets.length; i++) {
    while (buckets[i]) {
      // 可能有相同的值，所以要根据计数值递减来将元素放到结果数组中合适的位置
      arr[sortedIndex++] = i
      buckets[i]--
    }
  }

  return arr
}

运行如下图所示：

排序12

# 计数排序效率

时间复杂度是 $$O(n + k)$ $，其中k是临时计数数组的大小

# 桶排序

当数组中取值范围过大，或者不是整数时，可以使用桶排序来解决，其类似于计数排序创建的统计数组，桶排序需要创建若干个“桶“来协助排序。

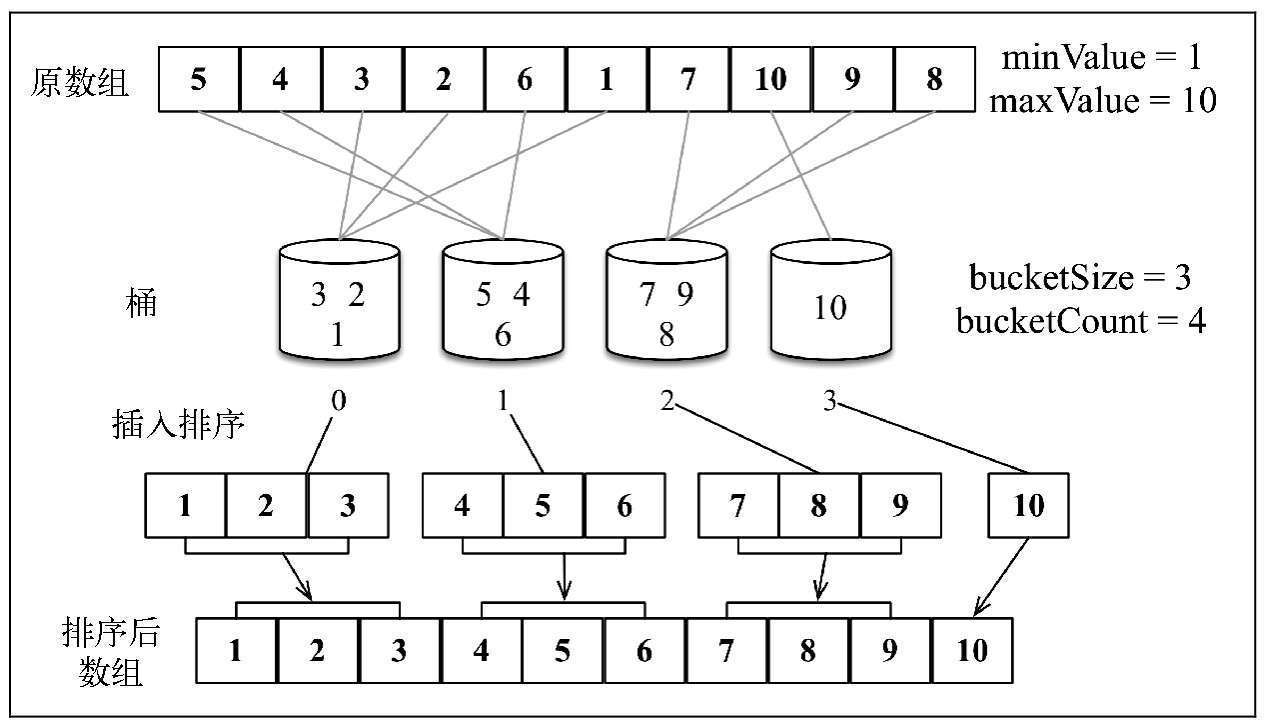
# 桶排序思路

每一个桶代表一个区间范围，里面可以承载一个或多个元素，首先我们要创建这些桶并明确每个桶的区间范围。区间大小 = （最大值 - 最小值）/ 桶的数量
遍历原始数组，把各元素放入各自的桶中
每个桶内的元素分别排序
遍历所有桶，输出所有元素

# 桶排序实现

/**
 * 桶排序
 * @param {*} arr 
 * @param {*} bucketSize 每个桶的大小
 * @returns 
 */
function bucketSort (arr, bucketSize = 5) {
  let min = Math.min(...arr)
  let max = Math.max(...arr)

  // 创建桶
  let bucketCount = Math.floor((max - min) / bucketSize) + 1 // 桶数量
  const buckets = new Array(bucketCount) // 初始化桶
  for (let i = 0; i < bucketCount; i++) {
    buckets.push([])
  }

  // 计算索引并放入桶中
  for (let i = 0; i < arr.length; i++) {
    const bucketIdx = Math.floor((arr[i] - min) / bucketSize)
    buckets[bucketIdx].push(arr[i])
  }

  // 桶数据排序
  const sortedArr = []
  for (let i = 0; i < buckets.length; i++) {
    // 插入排序
    sortedArr.push(...insertionSort(buckets[i]))
  }

  return sortedArr
}

排序如下图

排序13

# 桶排序效率

# 基数排序

基数排序也是一个分布式排序算法，它根据数字的有效位或基数（这也是它为什么叫基数排序）将整数分布到桶中。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

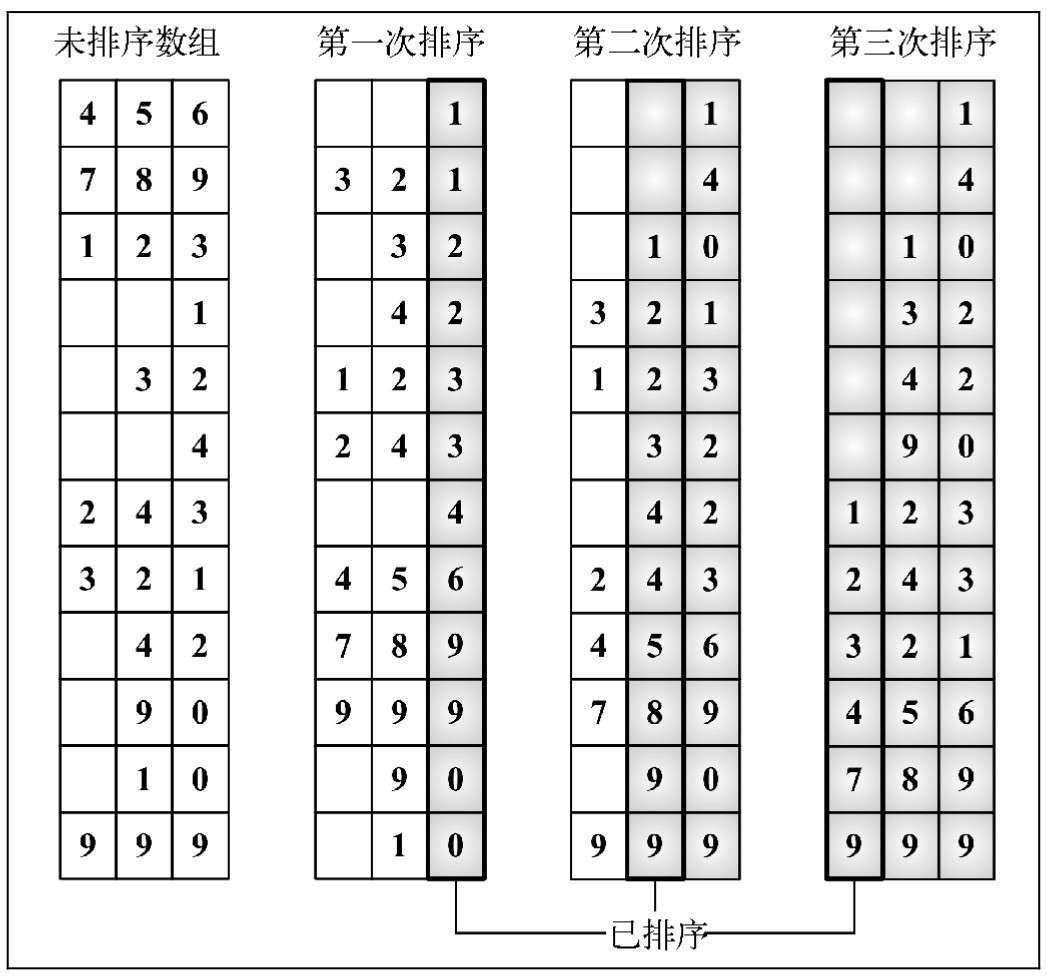
# 基数排序思路

先以个位数的大小来对数据进行排序，接着以十位数的大小来对数据进行排序，接着以百位数的，依此类推
在对某位数进行排序时，是用桶来排序的，排到最后，就是一组有序的元素
- 设置大小范围为0 - 9的10个桶，然后把具有相同的数值的数放进桶
- 再把桶里的数按照0到9号桶的顺序取出来，重复个位、十位、百位......
- 最后排序完成

# 基数排序实现

// 获得元素基于有效位应该插入的桶的索引
const getBucketIndex = (value, minValue, significantDigit, radixBase) =>
  Math.floor(((value - minValue) / significantDigit) % radixBase)

// 基于有效位的计数排序
const countingSortForRadix = (array, radixBase, significantDigit, minValue) => {
  let bucketsIndex
  const buckets = []
  const aux = []
  // 基于基数初始化桶
  for (let i = 0; i < radixBase; i++){
    buckets[i] = 0
  }
  // 基于数组中数的有效位进行计数排序
  for (let i = 0; i < array.length; i++){
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase)
    buckets[bucketsIndex]++
  }
  // 由于进行的是计数排序，还需要计算累积结果来得到正确的计数值,即累加后才能得出相应元素基于有效位排序后应该插入的正确索引
  for (let i = 1; i < radixBase; i++){
    buckets[i] += buckets[i - 1]
  }
  // 倒序遍历原始数组，将原始数组按有效位排序后相应的元素插入到新数组的正确索引
  for (let i = array.length - 1; i >= 0; i--){
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase)
    // 这里很关键，--buckets[bucketsIndex]就是该元素基于有效值排序后要插入的正确索引
    aux[--buckets[bucketsIndex]] = array[i]
  }
  // 将aux(排序好的)数组中的每个值转移到原始数组中
  for (let i = 0; i < array.length; i++){
    array[i] = aux[i]
  }
  return array
}

// 基数排序，根据数字的有效位或基数将整数分布到桶中
function radixSort(array, radixBase = 10) {
  if (array.length < 2) {
    return array
  }
  const minValue = Math.min(...array)
  const maxValue = Math.max(...array)
  // 对每一个有效位执行计数排序，从1开始
  let significantDigit = 1
  // 继续这个过程直到没有待排序的有效位
  while ((maxValue - minValue) / significantDigit >= 1) {
    array = countingSortForRadix(array, radixBase, significantDigit, minValue)
    significantDigit *= radixBase
  }
  return array
}

排序14

# 基数排序效率

时间复杂度：O(k∗n)

编辑

上次更新: 2022/01/25, 18:32:14

← 数据结构与算法-图数据结构与算法-总结→