CcbeanBlog
ccbean
2022-01-14
目录

数据结构与算法-图

# 数据结构与算法 - 图

在计算机程序设计中，图也是一种非常常见的数据结构，图论其实是一个非常大的话题，在数学上起源于哥尼斯堡七桥问题 (opens new window)。

图2

对于一个给定的连通图，如果存在超過两个（不包括两个）奇顶点，那么滿足要求的路線便不存在了，且有n个奇顶点的图至少需要n/2笔画出。如果只有兩個奇顶点，則可從其中任何一地出發完成一笔画。若所有点均为偶顶点，則從任何一点出發，所求的路線都能實現，他還說明了怎樣快速找到所要求的路線

不少數學家都嘗試去解析這类事例。而這些解析，最後發展成為了數學中的圖論。

# 图的概念

# 什么是图

图是一种与树有些相似的数据结构。

  • 实际上，在数学的概念上，树是图的一种。
  • 我们知道树可以用来模拟很多现实的数据结构，比如：家谱/公司组织架构等等。

图论是数学的一个分支，图论以图为研究对象，研究顶点和边组成的图形的数学理论和方法；

主要的研究目的为：事物之间的联系，顶点代表事物，边代表两个事物间的关系；

图的特点：

  • 一组顶点：通常用 V (Vertex) 表示顶点的集合
  • 一组边：通常用 E (Edge) 表示边的集合
  • 边是顶点和顶点之间的连线
  • 边可以是有向的，也可以是无向的。（比如 A --- B，通常表示无向。 A --> B，通常表示有向）

# 图的术语

图3

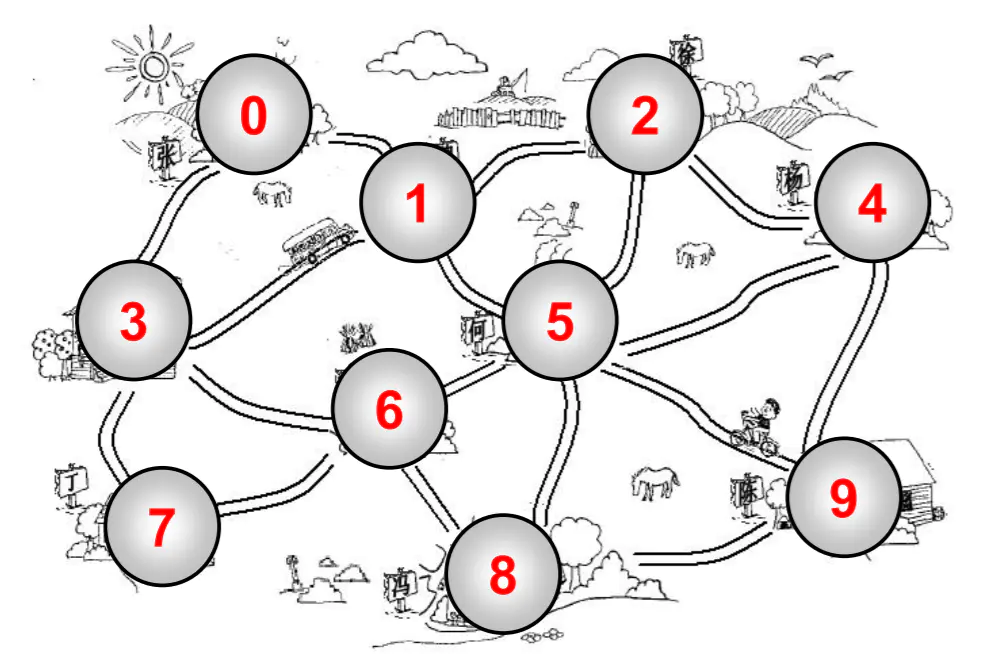
术语：

  • 顶点 V（Vertex）
    • 顶点刚才我们已经介绍过了，表示图中的一个结点。
    • 比如地铁站中某个站、多个村庄中的某个村庄、互联网中的某台主机、人际关系中的人。
  • 边 E (Edge)
    • 边表示顶点和顶点之间的连线。
    • 比如地铁站中两个站点之间的直接连线，就是一个边。
    • 注意：这里的边不要叫做路径，路径有其他的概念，后面会区分。
  • 相邻顶点
    • 由一条边连接在一起的顶点称为相邻顶点。
    • 比如 0 - 1 是相邻的，0 - 3 是相邻的。0 - 2 是不相邻的。
  • 度
    • 一个顶点的度是相邻顶点的数量
    • 比如 0 顶点和其他两个顶点相连，0 顶点的度是 2
    • 比如 1 顶点和其他四个顶点相连，1 顶点的度是 4
  • 路径
    • 路径是顶点 v1，v2...，vn 的一个连续序列, 比如上图中 0 1 5 9 就是一条路径。
    • 简单路径: 简单路径要求不包含重复的顶点. 比如 0 1 5 9 是一条简单路径。
    • 回路：第一个顶点和最后一个顶点相同的路径称为回路。比如 0 1 5 6 3 0。
  • 无向图
    • 上面的图就是一张无向图，因为所有的边都没有方向。
    • 比如 0 - 1 之间有边，那么说明这条边可以保证 0 -> 1，也可以保证 1 -> 0。
  • 有向图
    • 有向图表示的图中的边是有方向的。
    • 比如 0 -> 1，不能保证一定可以 1 -> 0，要根据方向来定。

下面这张图则是有向带权的图

图4

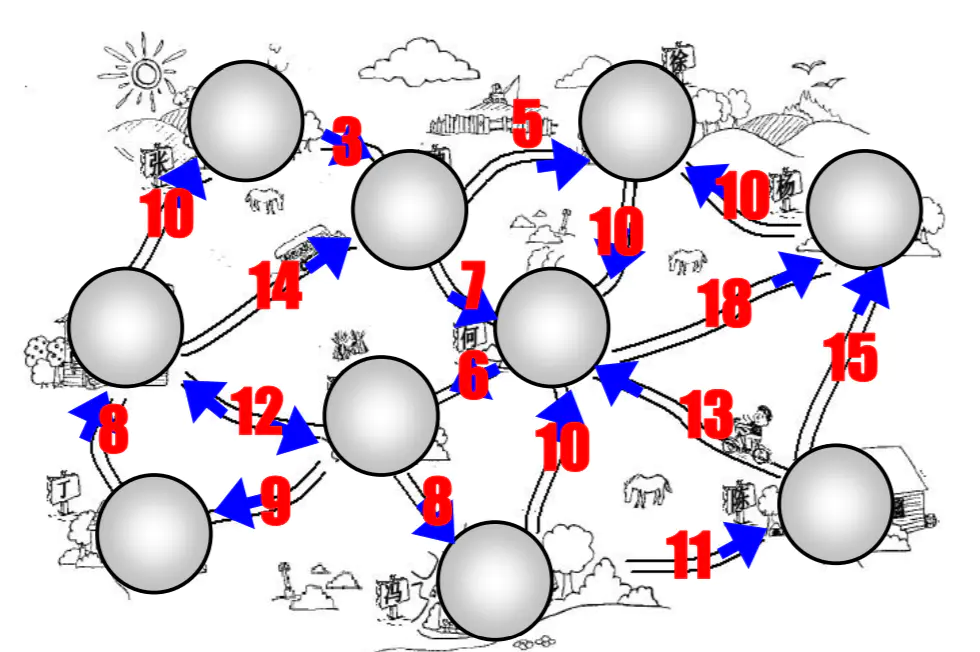
  • 无权图
    • 我们上面的图就是一张无权图（边没有携带权重）
    • 我们上面的图中的边是没有任何意义的，不能收 0 - 1 的边，比 4 - 9 的边更远或者用的时间更长。
  • 带权图
    • 带权图表示边有一定的权重
    • 这里的权重可以是任意你希望表示的数据：比如距离或者花费的时间或者票价。
    • 我们来看一张有向和带权的图

# 现实建模

  • 对交通流量建模
    • 顶点可以表示街道的十字路口，边可以表示街道。
    • 加权的边可以表示限速或者车道的数量或者街道的距离。
    • 建模人员可以用这个系统来判定最佳路线以及最可能堵车的街道。
  • 对飞机航线建模
    • 航空公司可以用图来为其飞行系统建模。
    • 将每个机场看成顶点，将经过两个顶点的每条航线看作一条边。
    • 加权的边可以表示从一个机场到另一个机场的航班成本，或两个机场间的距离。
    • 建模人员可以利用这个系统有效的判断从一个城市到另一个城市的最小航行成本。

# 图的表示

我们知道一个图包含很多顶点，另外包含顶点和顶点之间的连线（边），这两个都是非常重要的图信息，因此都需要在程序中体现出来。

# 顶点的表示

顶点的表示相对简单：

  • 上面的顶点，我们抽象成了 1 2 3 4，也可以抽象成 A B C D。在后面的案例中，我们使用 A B C D。
  • 那么这些 A B C D 我们可以使用一个数组来存储起来(存储所有的顶点)。
  • 当然，A B C D 有可能还表示其他含义的数据(比如村庄的名字)，这个时候，可以另外创建一个数组，用于存储对应的其他数据。

# 边的表示

边的表示略微复杂：

  • 因为边是两个顶点之间的关系，所以表示起来会稍微麻烦一些。
  • 可以使用邻接矩阵或邻接表来表示边

# 邻接矩阵

可以使用二维数组来表示邻接矩阵：

  • 邻接矩阵让每个节点和一个整数相关联，该整数作为数组的下标值；
  • 使用一个二维数组来表示顶点之间的连接；

图5

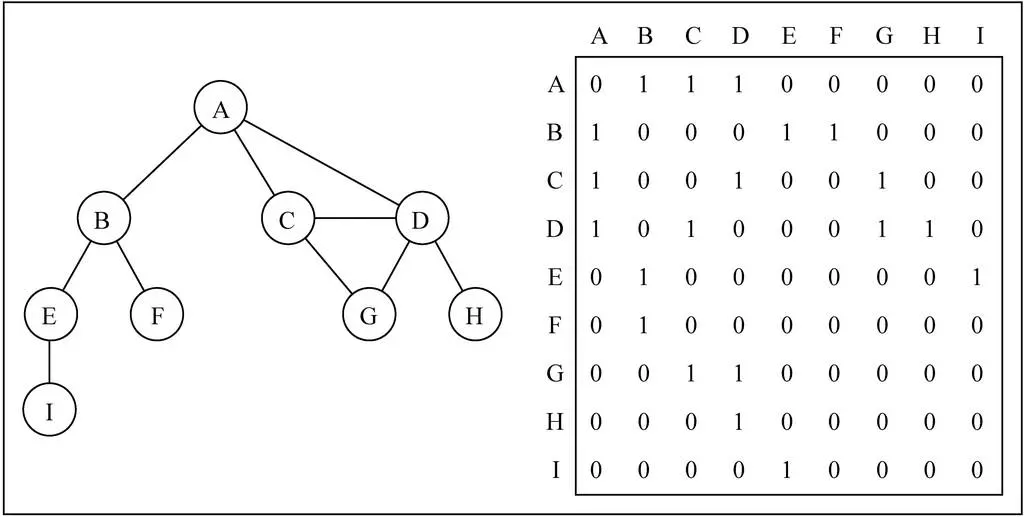
如上图所示：

  • 二维数组中的0表示没有连线，1表示有连线；
  • 如：A[ 0 ] [ 3 ] = 1，表示 A 和 C 之间有连接；
  • 邻接矩阵的对角线上的值都为0，表示A - A ，B - B，等自回路都没有连接（自己与自己之间没有连接）；
  • 若为无向图，则邻接矩阵应为对角线上元素全为0的对称矩阵；

邻接矩阵的问题：

  • 如果是一个无向图，邻接矩阵展示出来的二维数组，其实是一个对称图。
    • 也就是 A -> D 是 1 的时候，对称的位置 D -> 1 一定也是 1。
    • 那么这种情况下会造成空间的浪费
  • 如果图是一个稀疏图
    • 那么邻接矩阵中将存在大量的 0，造成存储空间的浪费；
    • 而且即使只有一个边，我们也必须遍历一行来找出这个边，也浪费很多时间。

# 邻接表

  • 邻接表由图中每个顶点以及和顶点相邻的顶点列表组成；
  • 这个列表可用多种方式存储，比如：**数组/链表/字典（哈希表）**等都可以；

图6

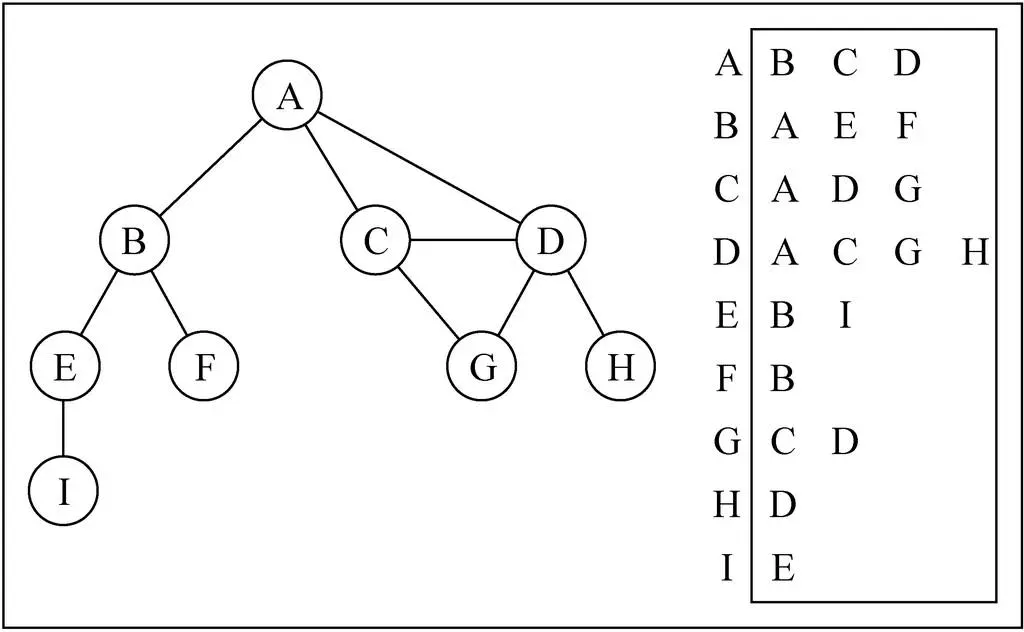
如上图所示：

  • 图中可清楚看到A与B、C、D相邻，假如要表示这些与A顶点相邻的顶点（边），可以通过将它们作为A的值（value）存入到对应的数组/链表/字典中。
  • 之后，通过键（key）A可以十分方便地取出对应的数据；

邻接表的问题：

  • 邻接表可以简单地得出出度 （出度：指向别人的数量，入度：指向自己的数量）
  • 但是，邻接表计算入度十分困难。此时需要构造逆邻接表才能有效计算入度；
  • 它必须构造一个“逆邻接表”，才能有效的计算“入度”。而邻接矩阵会非常简单。

# 图的封装

先创建图类Graph，并添加基本属性，再实现图类的常用方法：

创建一个数组对象vertexes存储图的顶点；创建一个字典对象edges存储图的边，其中key为顶点，value为存储key顶点相邻顶点的数组。

class Graph {
  constructor () {
    this.vertexs = [] // 顶点
    this.edges = new Dictionary() // 边
  }
}

# 添加方法

可以向图中添加一些顶点。

  • 将添加的顶点放入到数组中。
  • 另外，给该顶点创建一个数组[]，该数组用于存储顶点连接的所有的边。
addVertex (val) {
  this.vertexes.push(val)
  // 将边添加到字典中，新增的顶点作为键，对应的值为一个存储边的空数组
  this.edges.set(val, [])
}

添加边：可以指定顶点和顶点之间的边。

  • 添加边需要传入两个顶点，因为边是两个顶点之间的边，边不可能单独存在。
  • 根据顶点 v 取出对应的数组，将 w 加入到它的数组中。
  • 根据顶点 w 取出对应的数组，将 v 加入到它的数组中。
  • 因为这里实现的是无向图，所以边是可以双向的。
/**
 * 顶点添加边
 * @param {*} v1
 * @param {*} v2
 */
addEdge (v1, v2) {
  this.edges.get(v1).push(v2) // 取出字典对象edges中存储边的数组，并添加关联顶点
  this.edges.get(v2).push(v1) // 表示的是无向表，故要添加互相指向的两条边
}

# toString方法

为图类Graph添加toString方法，实现以邻接表的形式输出图中各顶点。

toString () {
  let res = ''
  for (let i = 0; i < this.vertexes.length; i++) {
    res += this.vertexes[i] + '->'
    let edges = this.edges.get(this.vertexes[i])
    for (let j = 0; j < edges.length; j++) {
        res += edges[j] + ' '
    }
    res += '\n'
  }
  return res
}

# 图的遍历

图的遍历思想与树的遍历思想一样，意味着需要将图中所有的顶点都访问一遍，并且不能有重复的访问（上面的toString方法会重复访问）

图的遍历有两种算法：

  • 广度优先搜索（Breadth - First Search，简称BFS）;
  • 深度优先搜索（Depth - First Search，简称DFS）;
  • 两种遍历算法都需要指定第一个被访问的顶点；

为了记录顶点是否被访问过，使用三种颜色来表示它们的状态

  • 白色：表示该顶点还没有被访问过；
  • 灰色：表示该顶点被访问过，但其相邻顶点并未完全被访问过；
  • 黑色：表示该顶点被访问过，且其所有相邻顶点都被访问过；
/**
 * 初始化顶点颜色
 * @returns 
 */
_initializeColor () {
  const colors = {}
  for (let i = 0; i < this.vertexes.length; i++) {
    colors[this.vertexes[i]] = COLOR.WHITE
  }
  return colors
}

# bfs

广度优先搜索算法的思路：

  • 广度优先搜索算法会从指定的第一个顶点开始遍历图，先访问其所有的相邻顶点，就像一次访问图的一层；
  • 也可以说是先宽后深地遍历图中的各个顶点；

图8

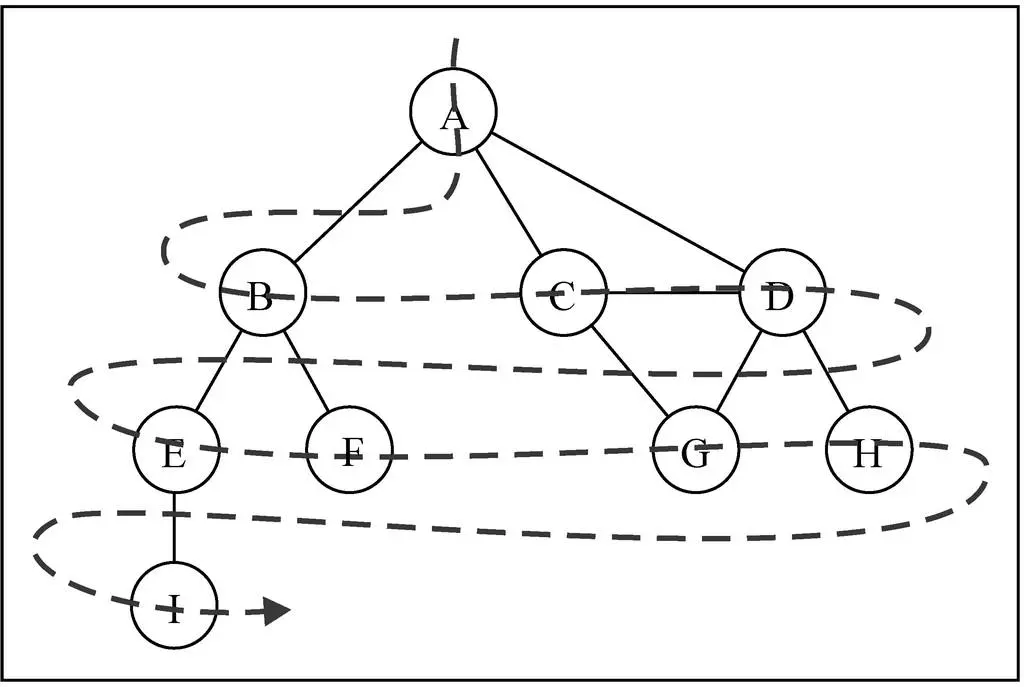
实现思路：

基于队列可以简单地实现广度优先搜索算法：

  • 首先创建一个队列Q（尾部进，首部出）；
  • 调用封装的_initializeColor方法将所有顶点初始化为白色；
  • 指定第一个顶点v，将v标注为灰色（被访问过的节点），并将v放入队列Q中；
  • 循环遍历队列中的元素，只要队列Q非空，就执行以下操作：
    • 先将灰色的v从Q的首部取出；
    • 取出v后，将v的所有未被访问过（白色）的相邻顶点依次从队列Q的尾部加入队列，并变为灰色。以此保证，灰色的相邻顶点不重复加入队列；
    • v的全部相邻节点加入Q后，v变为黑色，在下一次循环中被移除队列Q外；
/**
 * 广度优先搜索
 * @param {*} v 第一个顶点
 * @param {*} handler
 */
bfs (v, handler) {
  // 初始化顶点颜色
  const colors = this._initializeColor()

  const queue = new Queue()
  colors[v] = COLOR.GRAY // 置为灰色
  queue.enqueue(v) // 放入队列

  // 循环从队列中取出元素，队列为空则停止
  while(!queue.isEmpty()) {
    const qv = queue.dequeue()

    // qv的所有相邻顶点
    const qvNeighbours = this.edges.get(qv)

    // 将qv相邻顶点放入队列
    for (const neighbour of qvNeighbours) {
      if (colors[neighbour] === COLOR.WHITE) {
        // 未探测过的顶点，置为灰色，放入队列
        colors[neighbour] = COLOR.GRAY
        queue.enqueue(neighbour)
      }
    }

    // 顶点被访问过且被完全探测过 置为黑
    colors[v] = COLOR.BLACK

    if (typeof handler === 'function') {
      handler(qv)
    }
  }
}

下为指定的第一个顶点为A时的遍历过程：

  • 如 a 图所示，将在字典edges中取出的与A相邻的且未被访问过的白色顶点B、C、D放入队列que中并变为灰色，随后将A变为黑色并移出队列；

  • 接着，如图 b 所示，将在字典edges中取出的与B相邻的且未被访问过的白色顶点E、F放入队列que中并变为灰色，随后将B变为黑色并移出队列；

    图11

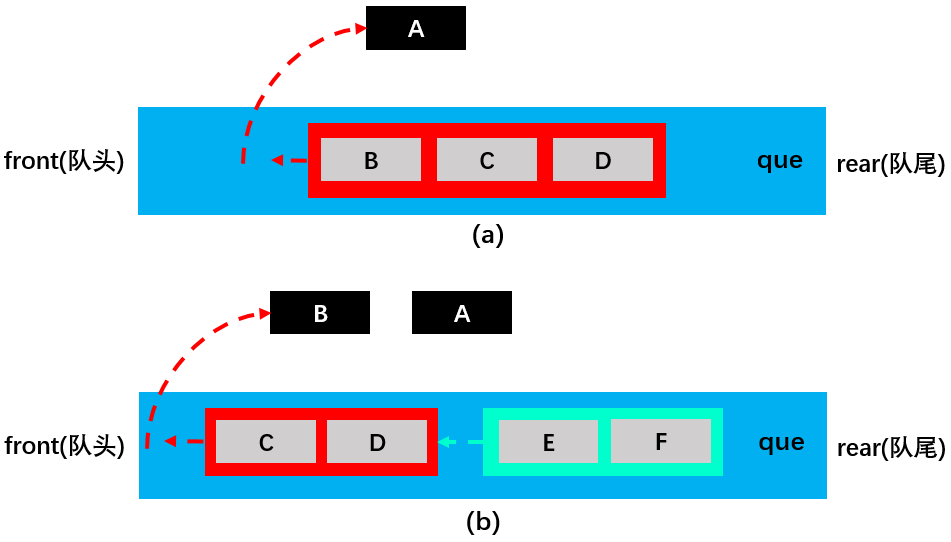
  • 如 c 图所示，将在字典edges中取出的与C相邻的且未被访问过的白色顶点G（A，D也相邻不过已变为灰色，所以不加入队列）放入队列que中并变为灰色，随后将C变为黑色并移出队列；

  • 接着，如图 d 所示，将在字典edges中取出的与D相邻的且未被访问过的白色顶点H放入队列que中并变为灰色，随后将D变为黑色并移出队列。

    图12

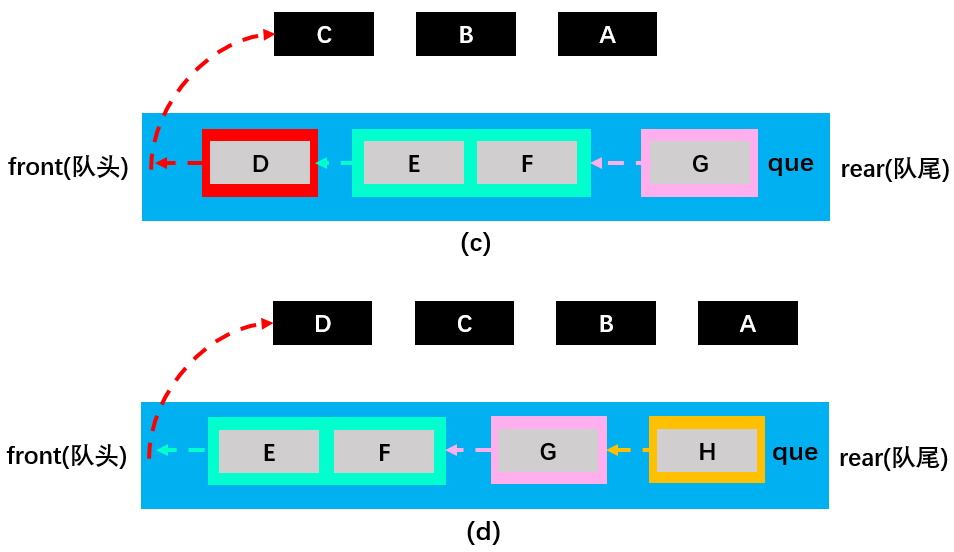
  • 如此循环直到队列中元素为0，即所有顶点都变黑并移出队列后才停止，此时图中顶点已被全部遍历。

# dfs

深度优先算法的思路：

  • 深度优先搜索算法将会从指定的第一个顶点开始遍历图，沿着一条路径遍历直到该路径的最后一个顶点都被访问过为止；
  • 接着沿原来路径回退并探索下一条路径，即先深后宽地遍历图中的各个顶点；

图9

实现思路：

  • 可以使用栈结构来实现深度优先搜索算法；
  • 深度优先搜索算法的遍历顺序与二叉搜索树中的先序遍历较为相似，同样可以使用递归来实现（递归的本质就是函数栈的调用）。

基于递归实现：

定义dfs方法用于调用递归方法dfsVisit，定义dfsVisit方法用于递归访问图中的各个顶点。

在dfs方法中：

  • 首先，调用initializeColor方法将所有顶点初始化为白色；
  • 然后，调用dfsVisit方法遍历图的顶点；

在dfsVisit方法中：

  • 首先，将传入的指定节点v标注为灰色；
  • 接着，处理顶点v；
  • 然后，访问v的相邻顶点；
  • 最后，将顶点v标注为黑色；
/**
 * 深度优先搜索 递归
 * @param {*} v
 * @param {*} handler 
 */
dfs (v, handler) {
  // 初始化顶点颜色
  const colors = this._initializeColor()

  this.dfsVisit(v, colors, handler)
}
/**
 * 遍历顶点
 * @param {*} v 
 * @param {*} colors 
 * @param {*} handler 
 */
dfsVisit (v, colors, handler) {
  colors[v] = COLOR.GRAY

  handler(v)
	
  // 访问指定顶点的相邻顶点
  const vNeighbours = this.edges.get(v)
  for (const neighbour of vNeighbours) {
    if (colors[neighbour] === COLOR.WHITE) {
      this.dfsVisit(neighbour, colors, handler)
    }
  }

  colors[v] = COLOR.BLACK
}

过程详解：

这里主要分析：访问指定顶点的相邻顶点。

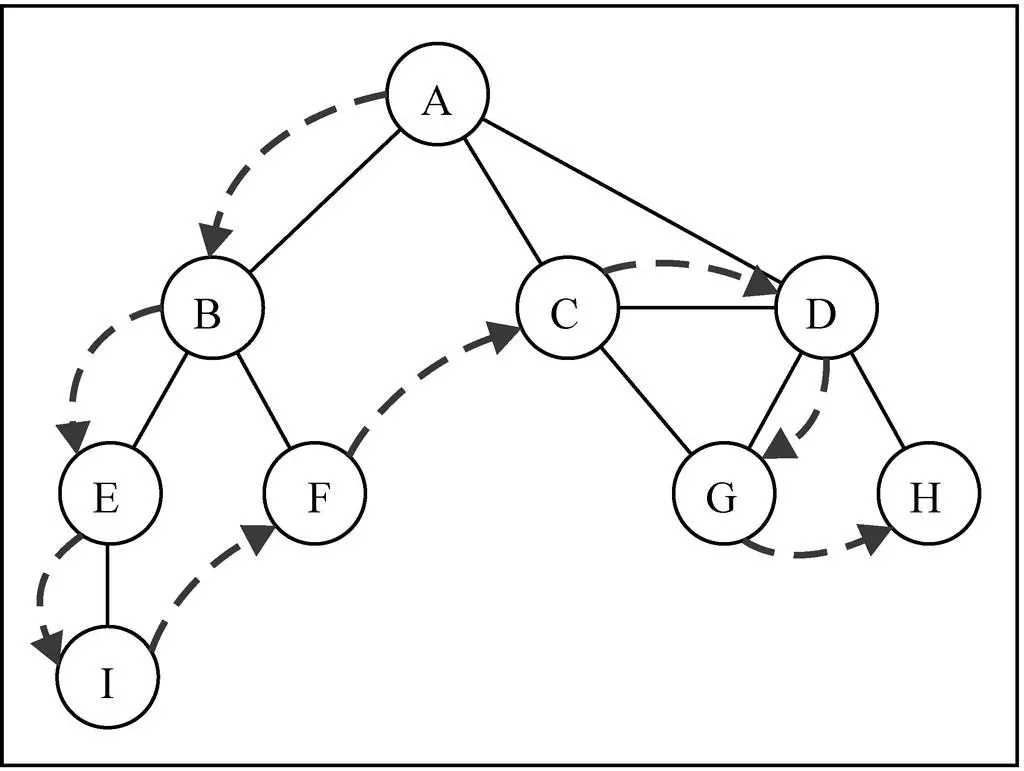
  • 以指定顶点A为例，先从储存顶点及其对应相邻顶点的字典对象edges中取出由顶点A的相邻顶点组成的数组：

    图13

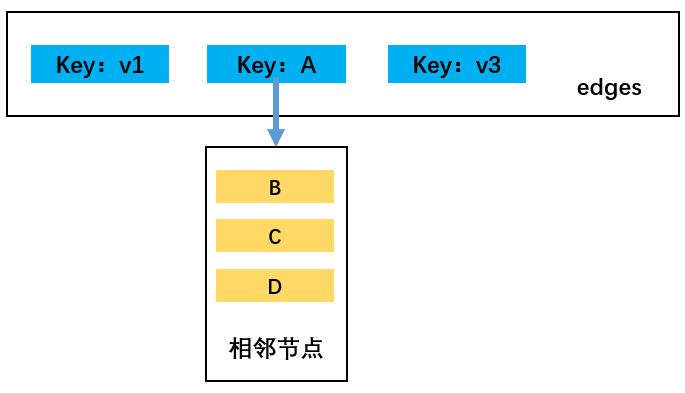
  • 第一步：A顶点变为灰色，随后进入第一个for循环，遍历A白色的相邻顶点：B、C、D；在该for循环的第1次循环中（执行B），B顶点满足：colors == "white"，触发递归，重新调用该方法；

  • 第二步：B顶点变为灰色，随后进入第二个for循环，遍历B白色的相邻顶点：E、F；在该for循环的第1次循环中（执行E），E顶点满足：colors == "white"，触发递归，重新调用该方法；

  • 第三步：E顶点变为灰色，随后进入第三个for循环，遍历E白色的相邻顶点：I；在该for循环的第1次循环中（执行I），I顶点满足：colors == "white"，触发递归，重新调用该方法；

  • 第四步：I顶点变为灰色，随后进入第四个for循环，由于顶点I的相邻顶点E不满足：colors == "white"，停止递归调用。过程如下图所示：

    图14

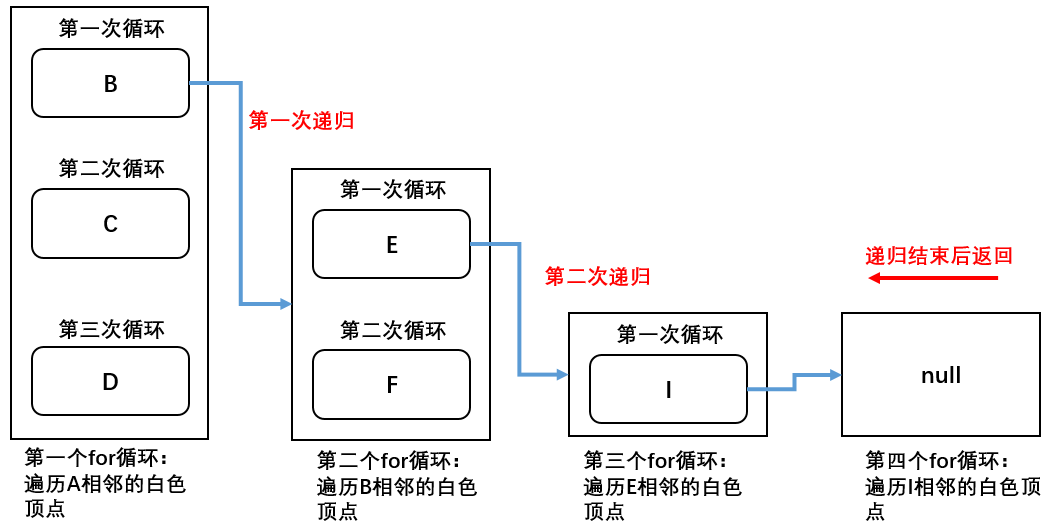
  • 第五步：递归结束后一路向上返回，首先回到第三个for循环中继续执行其中的第2、3...次循环，每次循环的执行过程与上面的同理，直到递归再次结束后，再返回到第二个for循环中继续执行其中的第2、3...次循环....以此类推直到将图的所有顶点访问完为止。

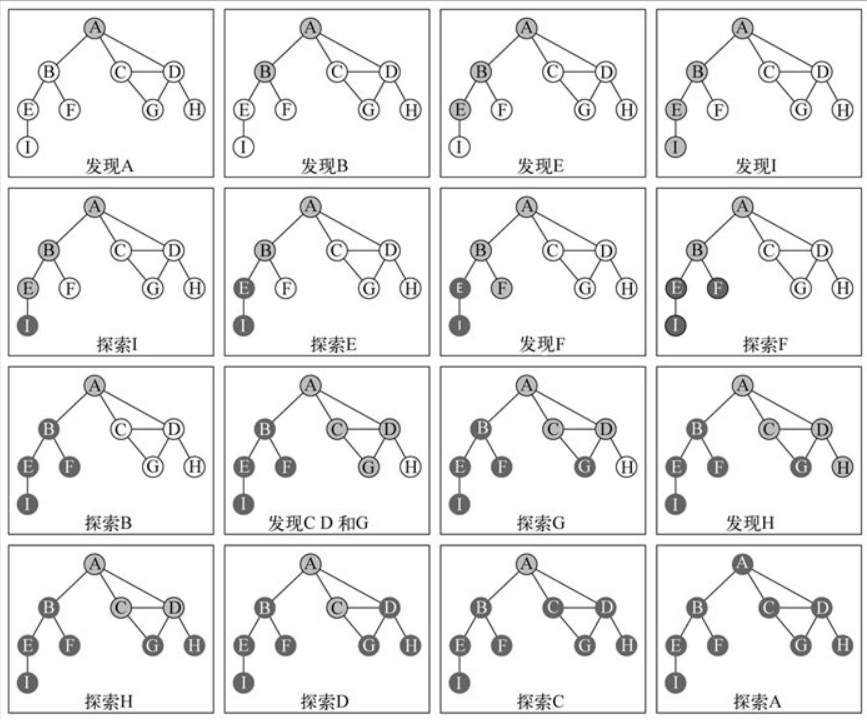
下图为遍历图中各顶点的完整过程：

  • 发现表示访问了该顶点，状态变为灰色；

  • 探索表示既访问了该顶点，也访问了该顶点的全部相邻顶点，状态变为黑色；

  • 由于在顶点变为灰色后就调用了处理函数handler，所以handler方法的输出顺序为发现顶点的顺序即：A、B、E、I、F、C、D、G、H 。

    图15

# 完整实现

const Dictionary = require('./Map')
const Queue = require('./Queue')
const Stack = require('./Stack')

const COLOR = {
  WHITE: 'white',
  GRAY: 'gray',
  BLACK: 'black'
}

module.exports = class Graph {
  constructor () {
    this.vertexes = [] // 顶点
    this.edges = new Dictionary() // 边
  }

  addVertex (val) {
    this.vertexes.push(val)
    // 将边添加到字典中，新增的顶点作为键，对应的值为一个存储边的空数组
    this.edges.set(val, [])
  }

  /**
   * 顶点添加边
   * @param {*} v1
   * @param {*} v2
   */
  addEdge (v1, v2) {
    this.edges.get(v1).push(v2) // 取出字典对象edges中存储边的数组，并添加关联顶点
    this.edges.get(v2).push(v1) // 表示的是无向表，故要添加互相指向的两条边
  }

  toString () {
    let res = ''
    for (let i = 0; i < this.vertexes.length; i++) {
      res += this.vertexes[i] + '->'
      let edges = this.edges.get(this.vertexes[i])
      for (let j = 0; j < edges.length; j++) {
          res += edges[j] + ' '
      }
      res += '\n'
    }
    return res
  }

  /**
   * 初始化顶点颜色
   * @returns 
   */
  _initializeColor () {
    const colors = {}
    for (let i = 0; i < this.vertexes.length; i++) {
      colors[this.vertexes[i]] = COLOR.WHITE
    }
    return colors
  }

  /**
   * 广度优先搜索
   * @param {*} v 第一个顶点
   * @param {*} handler
   */
  bfs (v, handler) {
    // 初始化顶点颜色
    const colors = this._initializeColor()

    const queue = new Queue()
    colors[v] = COLOR.GRAY // 置为灰色
    queue.enqueue(v) // 放入队列

    // 循环从队列中取出元素，队列为空则停止
    while(!queue.isEmpty()) {
      const qv = queue.dequeue()

      // qv的所有相邻顶点
      const qvNeighbours = this.edges.get(qv)

      // 将qv相邻顶点放入队列
      for (const neighbour of qvNeighbours) {
        if (colors[neighbour] === COLOR.WHITE) {
          // 未探测过的顶点，置为灰色，放入队列
          colors[neighbour] = COLOR.GRAY
          queue.enqueue(neighbour)
        }
      }

      // 顶点被访问过且被完全探测过 置为黑
      colors[v] = COLOR.BLACK

      if (typeof handler === 'function') {
        handler(qv)
      }
    }
  }

  /**
   * 深度优先搜索 递归
   * @param {*} v
   * @param {*} handler 
   */
  dfs (v, handler) {
    // 初始化顶点颜色
    const colors = this._initializeColor()

    this.dfsVisit(v, colors, handler)
  }
  /**
   * 遍历顶点
   * @param {*} v 
   * @param {*} colors 
   * @param {*} handler 
   */
  dfsVisit (v, colors, handler) {
    colors[v] = COLOR.GRAY

    handler(v)

    // 访问指定顶点的相邻顶点
    const vNeighbours = this.edges.get(v)
    for (const neighbour of vNeighbours) {
      if (colors[neighbour] === COLOR.WHITE) {
        // 相邻顶点为白色，递归调用函数继续访问
        this.dfsVisit(neighbour, colors, handler)
      }
    }

    colors[v] = COLOR.BLACK
  }
}

测试：

const Graph = require('../../lib/Graph') 

// 测试代码
let graph = new Graph()

// 添加顶点
let myVertexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
for (let i = 0; i < myVertexes.length; i++) {
  graph.addVertex(myVertexes[i])
}

// 添加边
graph.addEdge('A', 'B')
graph.addEdge('A', 'C')
graph.addEdge('A', 'D')
graph.addEdge('C', 'D')
graph.addEdge('C', 'G')
graph.addEdge('D', 'G')
graph.addEdge('D', 'H')
graph.addEdge('B', 'E')
graph.addEdge('B', 'F')
graph.addEdge('E', 'I')

console.log('toString', graph.toString())


// bfs
let bfsStr = ''
graph.bfs(graph.vertexes[0], (v) => {
  bfsStr += v + ' '
})
console.log(bfsStr)

// dfs
let dfsStr = ''
graph.dfs(graph.vertexes[0], (v) => {
  dfsStr += v + ' '
})
console.log(dfsStr)
编辑 (opens new window)
上次更新: 2022/03/01, 22:35:22
数据结构与算法-二叉堆
数据结构与算法-排序

← 数据结构与算法-排序→

最近更新
01
阅读精通正则表达式总结
09-29
02
项目搭建规范的配置
07-15
03
Vite的使用
07-03
更多文章>
Theme by Vdoing | Copyright © 2018-2023 Ccbeango