数据结构与算法-栈

栈是一种非常常见的数据结构，并且在程序中的应用非常广泛。

首先回顾下数组，数组是一个线性结构，并且可以在数组的任意位置插入和删除元素。但是有时候，我们为了实现某些功能，必须对这种任意性加以限制，栈和队列就是比较常见的受限的线性结构。

什么是栈

栈（stack）是一种运算受限的线性表：

• LIFO（last in first out）表示就是后进入的元素，第一个弹出栈空间。类似于自动餐托盘，最后放上的托盘，往往先把拿出去使用。
• 其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。
• 向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；
• 从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

如下图所示

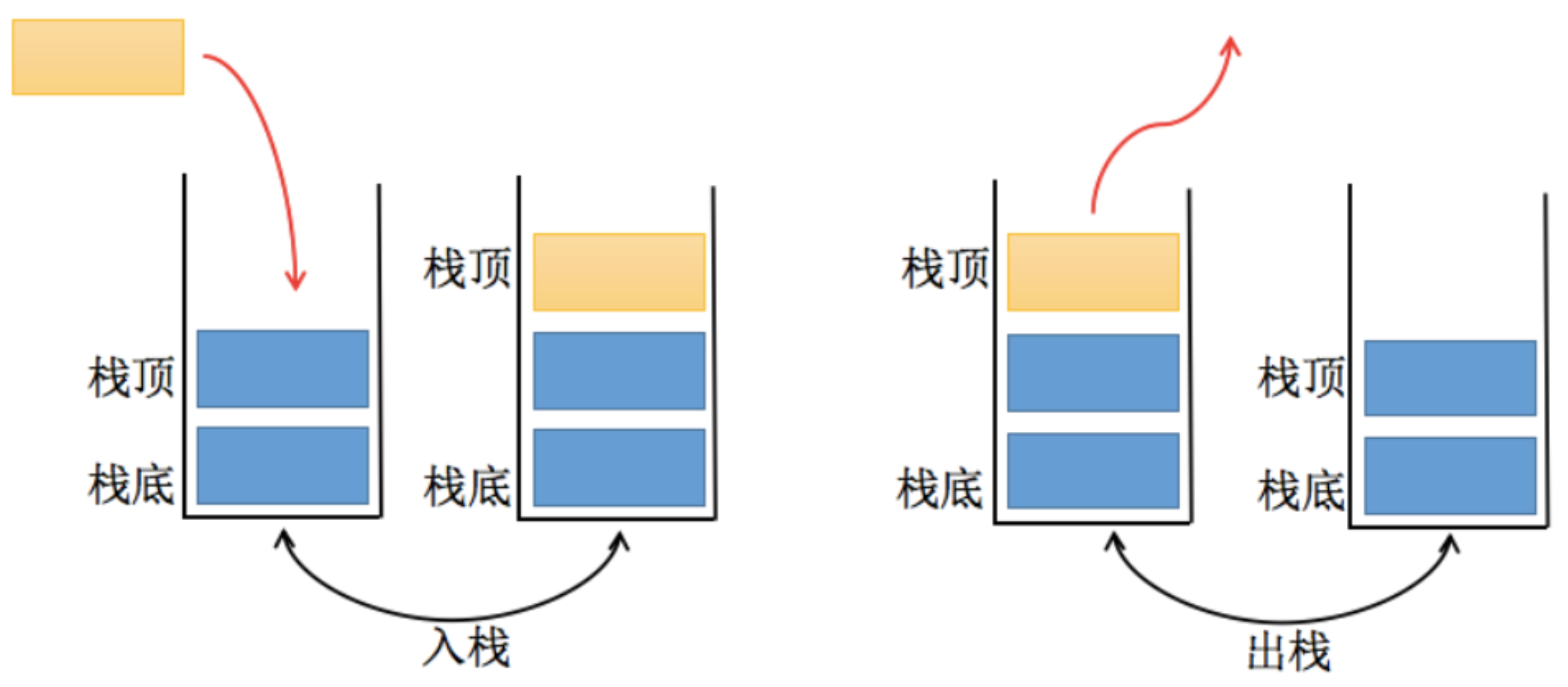
栈的特点是：先进后出，后进先出。

函数调用栈

函数调用栈，函数之间的相互调用，A调用B，B中又调用C，C中又调用D，即A(B(C(D())))。

1. 那样在执行的过程中， 会先将A压入栈， A没有执行完， 所有不会弹出栈。
2. 在A执行的过程中调用了B，会将B压入到栈，这个时候B在栈顶， A在栈底。
3. 如果这个时候B可以执行完，那么B会弹出栈。但是B没有执行完，它调用了C。
4. 所以C会压栈，并且在栈顶。而C调用了D，D会压入到栈顶。所以当前的栈顺序是: 栈底A->B->C->D栈顶。
5. 函数 D 执行完之后，会弹出栈被释放，弹出栈的顺序为 D->C->B->A。
6. 所以函数调用栈的称呼，就来自于它们内部的实现机制。(通过栈来实现的)

递归也是一个经典的函数调用栈，如果递归实现不当无限调用，会出现栈溢出的错误。为什么没有停止条件的递归会造成栈溢出？比如函数 A 为递归函数，不断地调用自己（因为函数还没有执行完，不会把函数弹出栈），不停地把相同的函数 A 压入栈，最后造成栈溢出（Queue Overfloat）。

还有中缀表达式转后缀表达式，也是利用了栈。

练习：

题目：有 6 个元素 6，5，4，3，2，1 按顺序进栈，问下列哪一个不是合法的出栈顺序？

• A：5 4 3 6 1 2 （√）

• B：4 5 3 2 1 6 （√）

• C：3 4 6 5 2 1 （×）

• D：2 3 4 1 5 6 （√）

解析：

• A 答案：65 进栈，5 出栈，4 进栈出栈，3 进栈出栈，6 出栈，21 进栈，1 出栈，2 出栈（整体入栈顺序符合 654321）
• B 答案：654 进栈，4 出栈，5 出栈，3 进栈出栈，2 进栈出栈，1 进栈出栈，6 出栈（整体的入栈顺序符合 654321）
• C 答案：6543 进栈，3 出栈，4 出栈，之后应该 5 出栈而不是 6，所以错误
• D 答案：65432 进栈，2 出栈，3 出栈，4 出栈，1 进栈出栈，5 出栈，6 出栈（整体入栈顺序符合 654321）

栈结构的实现

栈结构的实现有两种比较常见的方式，基于数组实现或基于链表实现。

我们基于数组来实现栈，对数组做一层包装，让它外层具有栈的特性，内部本质上还是数组。

栈常见的操作可总结如下：

• push(element): 添加一个新元素到栈顶位置.
• pop()：移除栈顶的元素，同时返回被移除的元素。
• peek()：返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它）。
• isEmpty()：如果栈里没有任何元素就返回true，否则返回false。
• clear()：移除栈里的所有元素。
• size()：返回栈里的元素个数。这个方法和数组的length属性很类似。
• toString()：将栈结构的内容以字符串形式返回。

代码实现：

/**
 * 栈 基于数组
 *  - 数组末尾的元素作为栈顶元素
 */
module.exports = class Stack {
  constructor () {
    // 存中所有元素存储
    this.items = []
  }

  // 添加一个新元素到栈顶位置
  push (element) {
    this.items.push(element)
  }

  // 移除栈顶的元素，同时返回被移除的元素
  pop () {
    return this.items.pop()
  }

  // 返回栈顶的元素，不对栈做任何修改
  peek () {
    return this.items[this.items.length - 1]
  }
  
  // 判断栈中是否有元素
  isEmpty () {
    return this.items.length === 0
  }

  // 移除栈中所有元素
  clear () {
    this.items = []
  }

  // 获取栈中元素个数
  size() {
    return this.items.length
  }
}

这里以数组末尾的元素作为栈顶元素。

测试

const numStack = new Stack()

// push
numStack.push(1)
numStack.push(2)
numStack.push(3)

console.log('push', numStack.items) // push [ 1, 2, 3 ]

// pop
console.log('pop', numStack.pop()) // pop 3

// peek
console.log('peek', numStack.peek()) // peek 2

// isEmpty
console.log('isEmpty', numStack.isEmpty()) // isEmpty false

// size
console.log('size', numStack.size()) // size 2

练习 — 十进制转二进制

我们可以使用栈来实现一个简单的例子，十进制转二进制。

• 把十进制转化成二进制，可以将该十进制数字和2整除（二进制是满二进一），直到结果是0为止

• 举个例子，把十进制的数字10转化成二进制的数字，过程大概是这样

  

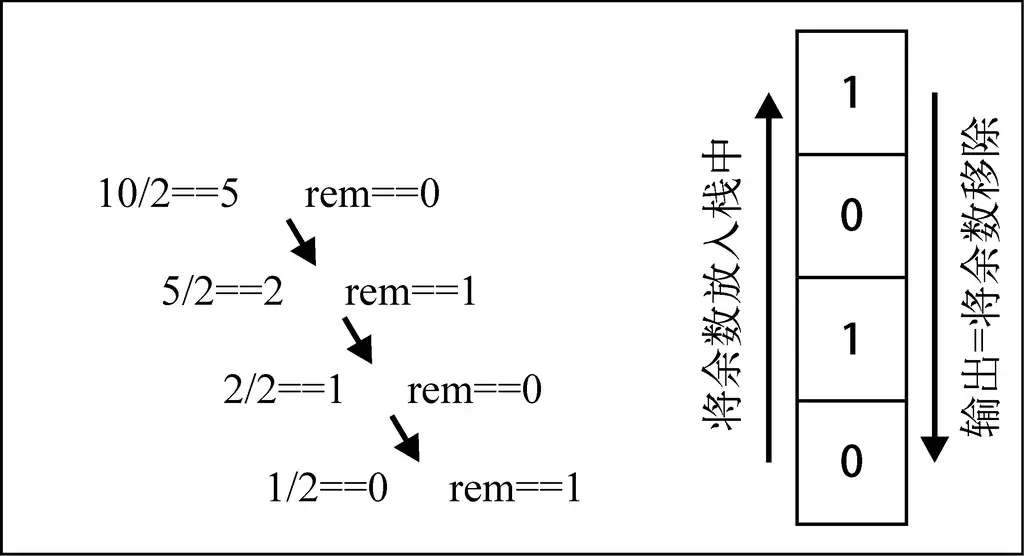
代码如下：

/**
 * 栈应用 十进制转二进制
 */
function dec2bin(decNumber) {
  const stack = new Stack() // 保存余数栈
  let remainer

  while (decNumber) {
    remainer = decNumber % 2
    decNumber = Math.floor(decNumber / 2)
    stack.push(remainer)
  }

  let binStr = ""
  while(!stack.isEmpty()) {
    binStr += stack.pop()
  }
  return binStr 
}

console.log(dec2bin(10)) // 1010
console.log(dec2bin(14)) // 1110
console.log(dec2bin(233)) // 11101001

最终的目的是拼接出二进制的字符串，这里只是为了使用栈做演示。

不需要使用栈

// 十进制转二进制
function dec2bin2(decNumber) {
  let binStr = ""

  let remainer
  while (decNumber) {
    remainer = decNumber % 2
    decNumber = Math.floor(decNumber / 2)

    binStr = `${remainer}${binStr}`
  }

  return binStr 
}

console.log(dec2bin(10)) // 1010
console.log(dec2bin(14)) // 1110
console.log(dec2bin(233)) // 11101001